Chapter 4 A catalogue of pedagogical patterns

4.1 Introduction

In this chapter, we present a collection of patterns that are particularly aligned with teaching and learning with Jupyter. Each pattern is targeted at specific learning goals, audiences, and teaching formats. With those in mind we describe each pattern and its pedagogical features that support the learning goals, present a practical example, and close each with any potential pitfalls you would want to be aware of.

4.2 Shift-Enter for the win

Description:
Instead of reading a static chapter about a topic, the learners read and execute code, as well as potentially interact with a widget to explore concepts. Starting from a complete notebook, the instructor or learner runs through the notebook cell-by-cell by typing SHIFT + ENTER.

Example:
The notebook (or a collection of notebooks) can be used as an alternative to a static textbook on a topic.

Learning goals:
This pattern can be used to introduce a topic or promote awareness about a set of tools. Additionally, it can serve as documentation that provides a tour of an application programming interface (API).

Audience(s):
Depending on the style of the notebook, this pattern can be used for a spectrum of programming abilities.

Format (lecture / lab / …):
This pattern can be used as an alternative to a static textbook. In a tutorial, a complete notebook can be used to provide a tour of an application programming interface (API) of a software package.

Features:
One benefit of this approach is that learners have a complete working example which they can adapt or build from. It provides opportunity for richer interaction than a static textbook.

Pitfalls:
This style does not prompt much engagement with students. Having a class that interactively works through a notebook can lead to some students finishing much faster than others (e.g., racing through SHIFT + ENTER). Breaking long notebooks into many smaller ones can help with the pacing in a lecture. Having a master notebook serve as the table of contents can then help students navigate through the class. Notebooks can be linked in a markdown cell as:

[Notebook 1](part1.ipynb)

4.3 Fill in the blanks

Description:
To focus attention on one aspect of a workflow, the scaffolding and majority of the workflow can be laid out and some elements removed with the intent that students (or the instructor during a demo) fill in those pieces. The exercise might be accompanied by a small test that the code should pass, or a plot, or value which the code should generate if correct.

Example:
A fundamental concept in computing is the use of a for loop to accumulate a result. A fill-in-the-blank exercise demonstrating an accumulator could lay out the initialization, provide the skeleton of the for loop and include plotting code, with the aim being that students write the update step inside the for loop.

Related patterns:
This pattern is similar to Target practice; a difference is that Target Practice often focuses on a bigger step in a multi-step process. Fill in the Blank exercises tend to be smaller and more immediate.

Learning goals:
This pattern focuses attention on a component of a task and provides the benefit of demonstrating how that component fits into the bigger picture or a larger workflow. It can be an effective approach for taking students on a tour of an API, requiring that they use the documentation of the software, or for focusing attention on one aspect of an multi-step computational model.

Audience(s):
This approach can be used with a range of students, from those who are first being introduced to computing concepts to those who have significant experience.

Format (lecture / lab / …):
Assignments and labs can adopt this approach (nbgrader can be used to help with marking). It can also be used in a lecture or tutorial setting where the instructor demos how to fill in the blank.

Pitfalls:
Some students don’t find this approach engaging. In particular, if the exercise is too simple for the level of programming competency of the students, it can be perceived as a “make-work” task.

4.4 Target Practice

Description:
The Target Practice pattern focuses the learner’s attention on one component of a multi-step workflow. The instructor provides all workflow steps except the one which is the focus of the exercise; the student will implement the “target” step within a notebook.

Example:
In a climate science assignment, the notebook that is given to students provides code for fetching and parsing 20 years of hourly average temperature data from a public database. Students are asked to design an algorithm for computing yearly average temperature and standard deviation. Following this, the plotting code which plots the yearly temperature with error-bars showing the standard deviation is also provided to the students.

Related patterns:
This pattern is similar to [Fill in the Blank] exercises. Fill in the Blank exercises are typically smaller and more immediate, while Target Practice exercises tend to be larger (e.g. an entire step in a multi-step process).

Learning goals:
The aim of a Target Practice exercise is to focus attention on one component of a workflow and practice skills for solving that component. It can also be used to reflect on broader consequences of choices made in the target step of an integrated workflow or analysis.

Audience(s):
This approach assumes some programming competency as learners are typically asked to start from scratch on the step that they are practicing.

Format (lecture / lab / …):
This approach is readily used in assignments or labs. It can also be used in an in-class demo where the instructor live-codes the missing component. It is beneficial if preceeding steps have been discussed in earlier lectures.

Pitfalls:
As there is more freedom in the implementation, this approach is typically more engaging than a Fill in the Blanks approach. However, starting from more of a “blank slate” can require more instructor input in order to get students started. Unit tests and pointers to useful library functions are often helpful, but may over-constrain the space of solutions, thereby reducing the level of creativity and problem solving expected from students. The amount of guidance should be carefully calibrated to the class and can be adjusted by giving tips in response to formative assessments. Working in small groups can help mitigate the risks of students having trouble getting started or pursuing tangents.

4.5 Tweak, twiddle, and frob

Description:
Students are given a notebook with a working example. They start by reading the text, running the code, and interpreting the results. Then they are asked to make a series of changes and run the code again; the changes can be small (tweaks), medium-sized (twiddles), or more substantial (frobs). For the origin of these terms, see The New Hacker’s Dictionary (Raymond, 1996).

Offering manipulations on a range of scales allows students to interact with notebooks in ways that suit their background and styles. Students who feel overwhelmed by the technology can get started with small, safe changes, enjoy immediate success, and work their way up. Students with more experience or less patience can make more radical changes and learn by “destructive testing”.

Examples:
In machine learning there are many steps to implementing an effective algorithm:

• Understand a problem
• Identify the proper machine learning algorithm to create the desired results
• Identify data and feature sets
• Optimize the configuration of the machine learning algorithms

We can write machine learning notebooks that allow students to modify parameters and interact at multiple levels of detail:

• twiddle hyper parameters to quickly see minor improvements in the results.
• tweak feature sets to create new models for a bigger impact
• frob by replacing the machine learning algorithm with a new algorithm or a new version

This pattern is particularly suitable for examples with a lot of parameters.

Learning goals:
This pattern helps students acquire domain knowledge by seeing the relationship between parameters and the effect they have on the results. It can also help students learn new notebook use patterns

This pattern is similar to “notebook as an app”; a difference is that in this pattern the code is more visible to the students, which can help orient them if they will make bigger changes in the future.

Audience(s):
This pattern can work with students who have no programming experience; they only need to be able to edit the contents of a cell and run a notebook. It can also work with students who have no background with the domain; they can learn about the domain by exploring the effect of parameters.

Format (lecture / lab / …):
This pattern lends itself to a workshop format, where students are guided through a notebook with time-boxed opportunities to experiment. It also lends itself to pair programming, where a navigator can suggest changes and a driver can implement them.

Features:
Can help students overcome anxiety about breaking code, and build comfort with self-directed exploration.

Pitfalls:
One hazard of this pattern is that students might have trouble getting started, so you might suggest a few examples; however, another hazard is that, if you provide examples, students will do what they are told and fail to explore. A third hazard is that the changes a student makes might be too unorganized; in that case the effect of the parameters might be lost in the chaos.

Enabling technologies:
Ideally the students should work in some kind of version control system that lets them revert to a previous version if they break something (and don’t know how to fix it). Note that undo and redo, Ctrl-z and Ctrl-y, can be used to traverse deep history within each cell, but not across cells.

4.6 Notebook as an app

Description:
Notebooks can be used to rapidly generate user interfaces where students and instructors can interact with code through sliders, entry boxes, and toggle buttons. The code can run numerical simulations or perform simple computations, and the output is often a graph or image.

Example:
In geophysics, a direct current resistivity survey involves connecting two electrodes to the ground through which current is induced. Current flows through the earth and the behavior depends upon the electrical resistivity of the subsurface structures; current flows around resistors and is channeled into conductors. At interfaces between conductors and resistors, charges build up, and these charges generate electric potentials which we measure at the surface of the earth. Each of these steps can be demonstrated through a simulation where students or the instructor builds a model, and views the currents, charges and electric potentials.

Related patterns:
Top-down sequence

Learning goals:
This approach can be effective for focusing on domain-specific knowledge and facilitating the exploration of models or computations.

Audience(s):
This style can be effective for students with minimal programming experience as they do not have to read, write, or see the code.

Format (lecture / lab / …):
In lecture, this style of notebook can be used by an instructor to methodically walk through a concept step-by-step. It is also useful for promoting in-class engagement as students can suggest different parameter choices and instructors can adapt the input parameters based on students’ questions.

In a lab or assignment, the notebook can be used as a “app” around which questions and exercises are built.

Features:
Notebooks as apps can be used to promote engagement with students in lecture. In labs, assignments or in-class activities, this approach lowers the barrier-to-entry for students to explore complex models.

Pitfalls:
It is important to have well-structured exercises and questions for students to address with the app. As with any app, simply asking students to play with it does not promote productive engagement.

In structuring an exercise for students, we recommend putting instructions and questions in a separate document rather than in the notebook. If students view the notebook as an app, they often want to interact with it rather than read it. By having instructions and questions that go alongside the notebook, they can have the app in view while reading.

This approach is not intended to be used for developing students’ programming skills.

Enabling technologies:
Widgets, domain-specific libraries such as simulation tools.

4.7 Win-day-one

Description:
A win-day-one exercise brings learners to the answer quickly and concisely, almost like a magic trick, and then breaks down and methodically works through each of the steps, revealing the magician’s tricks. It generally involves multiple notebooks: the first notebook being the “win” which shows the workflow end-to-end, and subsequent notebooks breaking down the details of each component of the workflow.

Example:
To solve a numerical simulation using a finite volume approach, a mesh must be designed, differential operators formed, boundary conditions set, a right-hand side generated and then the system solved. Naturally, there are important considerations for each step. For even a moderately sized problem, sparse matrices are necessary in order to keep memory usage contained, the mesh must be appropriately designed in order to satisfy boundary conditions, and the solver needs to be compatible with the structure of the system matrix. These details are critical for assembling a numerical computation, but if introduced upfront, they can overwhelm the conversation.

In a win-day-one approach, learners are first shown a concise example, in which many of the details are abstracted away in functions or objects. For example, methods such as get_mesh, get_pde, and solve abstract away the details of mesh design, creating differential operators and solving the set of equations. In subsequent notebooks, the workflow is tackled methodically, and the inner workings of each component discussed.

Related patterns:
Top-down sequence, Proof by example, disproof by counterexample

Learning goals:
This can be an effective approach for introducing complex processes, providing context for how each of the components fits together, and focusing attention.

Audience(s):
This style can be effective for a spectrum of student audiences from those with some programming experience to those with significant experience.

Format (lecture / lab / …):
This can be effective for tutorials and workshops, and can be used over multiple lectures. This can be useful when introducing new topics to help hook students because they accomplish significant results early in the learning process.

Pitfalls:
One hazard of the “win-day-one” is that the “win” is overwhelming (too much detail) or too magical (too little detail). An appropriate level of detail needs to be selected so that each of the components of the workflow is demonstrated, but at a high-level.

4.8 Top-down sequence

Description:
Particularly in STEM, the default sequence of presentation is bottom-up, meaning that we teach students how things work (and sometimes prove that they work), before students learn how to use them, or what they are for.

Notebooks afford the opportunity to present topics top-down; that is, students learn what a tool is for and how to use it, before they learn how it works.

Examples

• In digital signal processing, one of the most important ideas is the discrete Fourier transform, which depends on complex arithmetic; in a bottom-up approach, we would have to start by teaching or reviewing complex numbers, which is not particularly engaging.

  In contrast to writing the mathematics on paper, in a notebook students can use a library that does the discrete Fourier transform for them, so they understand what it is used for, and see the value of learning about it, before we ask them to do the work of understanding it.

• Some important methods are intrinsically leaky abstractions that require user expertise to use effectively and reliably. This is often because truly reliable solutions (if they exist) are disproportionately expensive for common cases. Numerical integration and methods for discretizing and solving differential equations often fall in this category. In addition to gaining intuition before diving into the details, the top-down pattern can be used to expose these leaks as motivation to understand the methods well enough to explain and correct for the shortcomings. For example, one can motivate convergence analysis and verification (Roache, 2004) by showing a solver that passes some consistency tests, but does not converge (or converges suboptimally) in general; or motivate conservative/compatible discretizations by showing a solver that has been verified for smooth solutions produce erroneous results for problems with singularities or discontinuities. Consider, for example, Gibbs and Runge phenomena, instability for Gram-Schmidt (Trefethen & Bau, 1997), entropy principles (LeVeque, 2002), eddy viscosity (Mishra & Spinolo, 2015), and LBB/inf-sup stability and “variational crimes” (Brenner & Scott, 2008; Chapelle & Bathe, 1993).

Learning goals:
This pattern is useful for building intuition, context, and motivation before introducing technical domain content instead of building up in a setting where implementation details often take center stage.

Audience(s):
This pattern can be effective with students who have limited programming skills, as they can use a library and see the results without writing much, if any, code.

Format (lecture / lab / …):
This pattern can be used in a single class session or homework, or spread out over the duration of a course; for example, students could use a tool on the first day and find out how it works on the last.

Features:
Shows students value and rewards their attention quickly (see Win-day-one).

Pitfalls:
A potential hazard of this pattern is that students might be less motivated to learn how the tool works if they think they have already understood what it is for and how to use it. This hazard can be mitigated by making obvious the additional benefit of understanding how it works (assuming that there actually is one—it is not enough to assert that knowing how it works is necessarily better). “Interesting” failure modes (see examples above) discovered by students while trying to solve a problem are great for motivating deeper understanding.

4.9 Two bites at every apple

Description:
This pattern involves writing an activity that can address multiple audiences from different perspectives at the same time. This can be powerful when addressing a mixed audience of students.

Example:
Say you have a group of students, some of whom are computer science students and some of whom are physics students, and ask them to come up with two expressions for computing the centroid of an area. The computer science students will be tasked with a description that involves adding up discrete pieces of areas with for loops and the physics students tasked with using the integral definition. When the students come up with their expressions they can then pair up with someone from the other background where they can attempt to explain how their approach matches the other and compare their final answers.

Learning goals:
Ability to translate from one field/language to another. Explain complex topics to someone from a different field.

Audience(s):
Groups which are composed of disparate backgrounds.

Format:
This format involves both individual and group work but can be used in a lab or lecture setting. The basic notebook would include an overview of the problem and then pose questions whose answer is the same but is worded for the different audiences. There can be a single notebook that contains both questions so that students can fill in their peers solution once they understand it or there can be separate notebooks for each group so they do not get distracted by the other question.

Features:
Group work and peer teaching has been shown to be effective at not only reinforcing student knowledge but also at introducing students to new concepts.

Pitfalls:
It can be difficult to construct questions for each audience that require equal amounts of difficulty.

4.10 Coding as translation

Description:
Converting mathematics to code is a critical skill today that many students, especially those without strong programming backgrounds, struggle to do. Explicitly taking an equation and translating it step-by-step to the code can help these students make the transition to attaining this skill.

Example:
Say you wanted to show the translation of matrix-vector multiplication from equation to a numerical computation. This would involve setting up and explaining the mathematics and suggesting replacing the sums with loops and initializing the sum properly.

Learning goals:
Translating mathematics to code (and vice versa)

Audience(s):
Learners who understand the theory but struggle with the programming side of things.

Format:
This type of pattern is often best served as a notebook with some explanatory text and possibly some scaffolded code so that a student can focus on the critical areas. This can be done as easily as a lab exercise or in lecture with perhaps some time held out for the students to solve it themselves before moving forward. It is critical to this pattern that there is a clear connection between the mathematical symbols (such as the summation) to the code (such as the for loops).

Features:
This pattern can work to lower the barrier for students with low programming knowledge to take on more complex tasks.

Pitfalls:
If the exercise is not properly scaffolded, namely it is too complex, students can be turned off. This is especially true if the code example is too complex with too many steps. For instance avoiding compound operators in the example above (+=) can help student retention.

4.11 Symbolic math over pencil + paper

Description:
Your objective is to convey an understanding of a physical system governed by a complicated mathematical system. Working out the algebra is necessary to uncover the fundamental behavior of the system, but how to do the algebra is not the goal of the lesson. In this case, you want to see the algebraic result and then teach the students the underlying meaning of the system,

Example:
The Euler equations for hydrodynamics are a system of partial differential equations governing conservation of mass, momentum, and energy. Their mathematical character admits wave solutions, and the eigenvalues and eigenvectors of the system in matrix form are important to understanding the physical behavior of the density, pressure, velocity, etc., in the system. Working out the eigenvalues with pencil and paper is tedious, and not the objective of the lesson. In this case, we can use a symbolic math library like SymPy (Meurer et al., 2017) to do the mathematical analysis for us, finding the eigenvalues and eigenvectors of the system, and we can then use this result to continue our theoretical discussion of the system.

Learning goals:
Students will see how to do symbolic math that arises in their theoretical analysis.

Audience(s):
STEM students that want to focus on understanding a mathematical system without worrying about the algebraic details.

Format:
This works well as a notebook that acts as a supplement to the main lecture. Since the goal of the lecture is the theory, the notebook can [TODO: complete]

Features:
Abstracts the details of mathematics that is secondary to the discussion at hand into a separate unit that students can explore on their own.

Pitfalls:
This only works well in the case that the algebra is not essential to the main learning goals, but rather is simply something that must be done to get to the main goal.

4.12 Replace analysis with numerical methods

Description:
Some ideas that are hard to understand with mathematical analysis are easy to understand with computer simulation and numerical methods.

In the usual presentation, students see and learn to do mathematical analysis on a series of simple examples, and resort to numerical methods only when necessary. In an alternative pattern, students skip the analysis and start with simulation and numerical methods, optionally visiting analysis after gaining practical experience.

Examples:
In statistics, hypothesis testing is a central idea that is notoriously difficult for students to understand. Students learn methods for computing p-values in a series of special cases, but many of them never understand the framework, or what a p-value means. The alternative is to compute sampling distributions and p-values by simulation; anecdotally, many students report that this approach makes the framework much clearer. Such simulation can also be used to drive home points about misconceptions held by most students and instructors (Haller & Krauss, 2002).

Similarly, in queueing theory, there are a few analytic results that apply under narrow conditions; when those conditions don’t apply, there are no analytic solutions. However, queueing systems lend themselves to simulation and visualization, and in simulation it is easy to explore a wide range of conditions.

And again, with differential equations, there are only a few special cases that have analytic solutions; the large majority of interesting, realistic problems don’t.

Learning goals:
This pattern is primarily about helping students see the big ideas of the domain more clearly, but it is also a chance to develop their programming skills. It also provides students with tools that are likely to be needed if they encounter similar problems in the real world, where analytic methods are often inapplicable, fragile, or complicated to use effectively.

Audience(s):
This pattern requires students to have some comfort with programming, although it would be possible for them to get some of the benefit from seeing examples without implementing them. Non-programmers can use this pattern via prepared notebooks; see Win Day One.

Format (lecture / lab / …):
This pattern can be used for in-class activities or homework.

Features:
Students can understand general ideas without getting bogged down in the details of special cases; and they are able to explore more interesting and realistic examples.

Pitfalls:
If students are not comfortable programmers, they can get bogged down in implementation details and debugging problems, and miss the domain content entirely. It is important to scope the implementation effort to suit the full range of students in the class. Pair programming can help mitigate these problems, especially if every pair has at least one student with programming skills, and if students are coached to pair program effectively (without letting the more experienced student dominate).

4.13 The API is the lesson

Description:
When students work with a software library, they are exposed to functions and objects that make up an application programming interface (API). Learning an API can be cognitive overhead; that is, material students have to learn to get work done computationally, but which does not contribute to their understanding of the subject matter. But the API can also be the lesson; that is, by learning the API, students are implicitly learning the intended content.

Example:
In digital signal processing, one of the most important ideas is the relationship between two representations of a signal: as a wave in the time domain and as a spectrum in the frequency domain. Suppose the API provides two objects, called Wave and Spectrum, and two functions, one that takes a Wave and returns a Spectrum, and another that takes a Spectrum and returns a Wave. By using this API, students implicitly learn that a Wave and a Spectrum are equivalent representations of the same information; given either one, you can compute the other.

Related patterns:
Top-down sequence

Learning goals:
This pattern is useful for shifting students’ focus from implementation details to domain content.

Audience(s):
This pattern is most effective if students have some experience using libraries and exploring APIs.

Format (lecture / lab / …):
This pattern TODO: complete

Pitfalls:
A hazard of this pattern is that students sometimes perceive the costs of learning the API and do not perceive the benefits. It might be necessary to help them see that learning the API is part of the lesson and not just overhead.

4.14 Proof by example, disproof by counterexample

Description:
In many classes, students see general results derived or proved, and then use those results in programs. Notebooks can help students understand how these results work in practice, when they apply, and how they fail when they do not.

Example:
In statistics, the Central Limit Theorem (CLT) gives the conditions when the sum of random variables converge to a Gaussian distribution. Students can generate random variables from a variety of distributions and test whether the sums converge and how quickly.

The classical Gram–Schmidt is unstable while the modified method is stable. Students can find matrices for which this instability produces obviously unusable results. They can also find matrices for which modified Gram-Schmidt produces unusable results due to its lack of backward stability, and this can be used to motivate Householder factorization and discussion of backward stability.

Some numerical methods for PDE converge with an assumption on smoothness of coefficients. Students can show how violating these assumptions leads to erroneous solutions, thus motivating discussion of conservative/compatible methods that can converge in such circumstances.

Learning goals:
This pattern is primarily useful for developing mathematical or domain knowledge, but students might also develop programming experience by writing code to run the examples and test the outcomes. This is especially true if the space of (counter-)examples is “small”, such that principled exploration (e.g., by finding an eigenvector, running an optimization algorithm, or searching a dictionary) is beneficial.

Audience(s):
This pattern requires students to have some programming experience.

Format (lecture / lab / …):
This pattern can be used for in-class activities or homework.

Features:
Helps students translate from theoretical results to practical implications, and to remember the assumptions and limitations of theory.

Pitfalls:
This pattern requires additional time and student effort on a topic that might not deserve the additional resources.

4.15 The world is your dataset

Description:
Notebooks provide several ways to connect students with the world beyond the classroom: one simple way is to collect data from external sources. Data is available in many different formats that require different software tools to collect and parse.

If a dataset is available in a standard format, like CSV, it can be downloaded from inside the notebook, which demonstrates a good practice for data integrity (going to the source rather than working with a copy) and demystifies the source of the data.

For data in tabular form on a web page, it is often possible to use Pandas to parse the HTML and generate a DataFrame. Also, for less structured sources, tools like Scrapy can be used to extract data, “scrape”, from sources that would be hard to collect manually, and to automate cleaning and validation steps.

Examples:
Datasets like the National Survey of Family Growth are available in files that can be downloaded directly from their website, but the terms of use forbid redistributing the data. So the best way for an instructor to share this data is to provide students with code to input into a notebook cell, which, when executed, will download the data set the first time the student runs the notebook.

Many Wikipedia pages contain data in HTML tables; most of them can be imported easily into a notebook using Pandas.

Sources of sports-related statistics are often embedded in large networks of linked web pages. Tools like Scrapy can navigate these networks to collect data in forms more amenable to automated analysis.

Audience(s):
Students with limited programming experience can work with datasets in standard formats, but scraping data might require more programming experience.

Format (lecture / lab / …):
This pattern lends itself to more open-ended project work where students are responsible for identifying data sources, collecting data, cleaning, and validating, but it can be adapted to more scaffolded work (see Target Practice).

Features:
Contributes to students’ feelings of autonomy and connectedness.

Pitfalls:
A hazard of this pattern is that students can spend too much time looking for data that is not available. They might need coaching about how to make do with the data they can get, even if it is not ideal.

Enabling technologies:
Pandas, Scrapy, R, ROpenSci packages

4.16 Now you try (with different data or process)

Description:
Students start with a complete working example provided by an instructor and then they change the dataset or process to apply the notebook to an area of their own choosing. This method can allow more or less fluctuation depending on the skills of the students. For example we can allow students to select new datasets from a list that ensures the cells of the notebook will all still work or we can give them freedom to try new data structures or add new processes to break the notebooks and learn as they go through the process of fixing the broken cells.

Example:
An instructor designs a lesson in exploratory data analysis to scrape the critics’ reviews for a specific movie from a particular movie review website and then provide some simple visualizations. The students have a few options:

1. Green Circle - replace the movie name and pick any movie they want and then step through the new notebook and see the new results.
2. Blue Square - adjust the notebook to scrape users’ reviews rather than critics’ reviews and then fix any data parsing problems.
3. Black Diamond - add different visualizations tailored to explore the user reviews (as opposed to the initial visualizations that are tailored for the critics’ reviews).

There are various ways to test the properties of numerical methods. For example, students can use the method of manufactured solutions to test the order of accuracy for a differential equation solver. They can also measure cost as the resolution is increased and present the results in a way that would help an analyst decide which method to use given external requirements (e.g., using accuracy versus cost tradeoff curves).

Related patterns:
Top-down sequence

Learning goals:
This pattern allows students to apply their knowledge

Audience(s):
This pattern can be tailored for students with more or less experience even in the same course.

Format (lecture / lab / …):
This pattern is best in a lab or an interactive tutorial

Pitfalls:
A hazard of this pattern is that students may go completely off the rails and chose datasets or new processes that have not been tested and will not work in the timeframe allowed.

4.17 Connect to external audiences

Description:
This is in some sense the opposite of “the world is your dataset.” Here the goal is to take a workflow or computational exploration and share it with the world so others can see it, learn from it, reuse and remix it.

Examples:
Your students are doing an observational astronomy lab where they take data from a telescope of a transiting exoplanet (a planet around a star other than our Sun) and they examine the lightcurve to learn about the planet. The students present the lab as a Jupyter notebook with a reproducible workflow that starts with reading in their data (images), walks through cleaning and reducing the images, and then performs photometry on the host star to produce a lightcurve. The end product is a plot showing the star’s brightness, dimming just slightly as the unseen planet comes between the star and earth. Elated with their result, the students want to share their data and workflow so anyone else can redo the analysis.

Learning goals:
Reproducibility is an important part of the scientific process. Having completed the primary scientific analysis that was the goal of the lab (obtaining a lightcurve of a transiting exoplanet), the students now can learn reproducible science practices by hosting their notebook on a webserver (e.g., Github) along with the data. An essential part of making the notebook reproducible will be ensuring that the notebook clearly lists the needed dependencies.

Audience(s):
All students—everyone should learn about reproducibility.

Format:
A self-contained notebook hosted on a webserver.

Features:
Teaches students about reproducible science workflows.

Pitfalls:
You need to be clear about the library requirements needed to run the notebook. Also, since the data files are likely separate from the notebook, it is possible for copies of the notebook to get shared without the data. Students may also be shy or fearful of showing their work publicly, so explaining the benefits may be needed to curtail their worries.

4.18 There can be only one

Description:
This pattern involves creating a competition between individual students or teams of students. Clear goals and metrics need to be defined and then students submit notebooks that are scored and evaluated. Competitions can span months or be completed in a single class.

The Jupyter ecosystem support for reproducibility and data sharing make it a great environment for creating healthy competitions. Kaggle is a site that hosts many machine learning competitions using Jupyter as its underlying infrastructure and is a great place for advanced students to extend their knowledge with a chance of winning cash prizes and solving current world problems.

Examples:
Identify a machine learning problem and a labeled dataset your students can use to train their model. Then select an evaluation metric and detail your problem statement and rules. Finally, launch your competition and allow your students to submit their notebooks and post their results on a public leaderboard.

Learning goals:
Creative problem solving is a key aspect of this pattern. In addition, if the competition is team-based then the students will learn how to work in groups and communicate effectively and share responsibilities.

Audience(s):
Students can benefit from healthy competition and working in teams, however it is critical that a safe, fun, and engaging environment is created. Advanced students can be pointed toward kaggle or other public competitions that may be in their area of interest and give them a chance to test their skills in the real world.

Format:
A competition can be defined with any metrics and rules and can be run in multiple ways. The students can help define the rules or a simple vote can decide the winners. For a more formal competition instructor can host free competitions for their class hosted by Kaggle. https://www.kaggle.com/about/inclass/overview

Features:
Teaches students about creative problem solving and teamwork.

Pitfalls:
Creating a fair competition is not trivial and considerations regarding data, metrics, rules, and scoring may be time consuming. Competition is risky business and effort should be made to ensure both winners and losers enjoy the experience.

4.19 Hello, world!

Description:
In some situations (such as the first day of class of a very introductory course) you may wish to do no more (and no less) than build confidence in the students’ abilities to be able to write a first computer program. Traditionally, the first program written was a “hello, world” program: a program that did nothing but display the text “hello, world” on the screen. However, these days students can have much more fun, and step fully into the creative world of computing with very little instruction.

Example:
Draw a rectangle. Change the numbers, run it again, and see what happens.

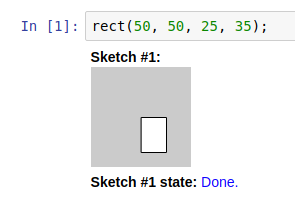
Figure: a first sketch using Calysto Processing, a Java-based language designed for creating art.

Learning goals:
Reduce stress, build confidence, connect onto their personal lives. Requires that they do learn the basics of Jupyter including: log in, open a new notebook, enter the provided code, and execute it. Often leads to a very animated, active learning classroom activity (“How can I change the colors?”, “How do I draw a circle?”, etc.)

Audience(s):
Beginning students.

Format (lecture / lab / …):
First day of class, in-class exercise. Build on what students already know from typing and reading (e.g., cut and paste, read top-to-bottom).

Features:
Open ended, creative, fun.

Pitfalls:
Works best when used with a pre-installed Jupyter (see the relevant chapter). Rather than telling students that they can do it, just do it. As a first assignment, to cut down on the vast possibilities, we suggest limiting the palette of options. For example, restrict their drawings to use only a single shape, such as rectangle or triangle. We suggest having the students draw something in their life that is important or meaningful to them. We suggest discussing the coordinate grid for the first assignment and sketching an idea on paper first.

4.20 Test driven development

Description:
The instructor provides tests written in a unit testing framework like unittest or doctest; students write code to make the tests pass.

Example:
TODO: Necessary?

Learning goals:
Helps students learn a good software development process.

Audience(s):
This pattern requires students to have some programming experience.

Format (lecture / lab / …):
This pattern can be used for in-class activities or homework.

Features:
Helps students focus on the task at hand and know when they are done (at least to the degree that the tests are complete).

Pitfalls:
Some Python unit testing frameworks are not designed to work with notebooks, and can be awkward to use. On the other hand, nbgrader [TODO: add cross reference to nbgrader] supports automated testing of the code students write in notebooks; in that environment, the tests are not visible to students, which may or may not be a bug.

This pattern requires the overhead of teaching students about the unit testing framework. Students working to make tests pass can lose their view of the big picture, and feel like they have been robbed of autonomy. This type of exercise is best used sparingly.

4.21 Code reviews

Code reviews involve a student or instructor providing feedback on someone else’s code. This pattern involves peer work as well as a means for providing feedback to students on topics other than correctness of their code but also on code readability and styling.

Example:
Present a problem to students that they must write a solution to, say computing the square root of a number without using a built-in function but have them write a test for their function that uses a built-in function to compute the answer. After they are finished have the students pair up and perform peer reviews of each other’s code, commenting not only on the way they solved the problem, such as making up a list of pros and cons of their approaches, but also on the readability of the code.

Learning goals:
Learn to read and understand someone else’s code. Learn to write readable code.

Audience(s):
Any group of students who are involved in coding.

Format:
Once a suitable problem is formulated in a notebook (or simply a script) then in-class review, as with the above example, can work for peer reviews. Alternatively students can upload their notebooks/scripts to a platform such as GitHub and the code reviews can be done using the tools available there. Sufficient scaffolding must be provided so that students understand the process, how to make constructive comments and why the process is important. If an instructor wants to review and provide feedback notebooks/scripts can be collected and commented on with a similar explanation to students as to how they are going to be graded (if they are).

Features:
This pattern leads to not just feedback for the person who wrote the code but also for the reader. Code review is also a critical piece of the software development process used in industry providing students with a view of the process. This can also have the result of making sure that a student’s code is readable via appropriate code styling, commenting and documentation.

Pitfalls:
Students need to be properly informed as to how the code reviews will impact their grades, especially if peer review is used. Notebooks on GitHub are not as easily reviewed as scripts.

4.22 Bug hunt

Description:
The instructor provides a notebook with code that contains deliberate bugs. The students are asked to find and fix the bugs. Automated tests might be provided to help students know whether some bugs remain unfixed.

Example:
TODO

Learning goals:
This pattern helps students develop programming skills, especially debugging (of course); it also gives the practice reading other people’s code, which can be an opportunity to demonstrate good practice, or warn against bad practice. It can also be used to teach students how to use debugging tools.

Audience(s):
This pattern requires students to have some programming experience.

Format (lecture / lab / …):
This pattern can be used for in-class activities or homework.

Features:
Can be engaging and fun; develops important meta-skills.

Pitfalls:
The bugs need to be calibrated to the ability of the students: if they are too easy, they are not engaging; if they are too hard, they are likely to be frustrating.

4.23 Adversarial programming

Description:
This pattern involves participants writing a solution to a problem and tests that attempt to make the written solution fail. This pattern can be done in many ways including having students complete the tasks and pair up and exchange solutions/tests or having the instructor writing the solution and the students then write the tests.

Example:
Students are tasked to write a function that finds the roots of a polynomial specified via some appropriate input. They are also asked to write a set of tests that their function passes and fails on. When students have completed these tasks they then exchange their notebooks and use the tests they wrote on their peer’s function. Finally they will discuss any differences in their approaches and whether they can come up with ways to not fail each other’s tests or if the tests provided are invalid.

Learning goals:
Learn to write unit tests. Think critically on how an adversary might break their solution.

Audience(s):
Any group of students who are involved in coding.

Format:
Decide on a sufficiently complex problem that may have non-trivial tests written for it and write up the question in a notebook. Then as an in-class activity or lab start the discussion regarding the tests. If appropriate the instructor can collect notable tests written by students and also share those.

Features:
Provides a means for students to think critically about a problem they are solving and how someone might break their solution. Also can provide a learning activity with a form of competition involved, which can then lead to an award system if desired.

Pitfalls:
With competition come dangers if students are not properly scaffolded so that they can provide constructive feedback. Some problems and/or solution strategies are vulnerable to many corner cases, leading to tedious whack-a-mole or fatalism that may distract from learning objectives.

References

Brenner, S. C., & Scott, L. R. (2008). The mathematical theory of finite element methods. Springer Verlag.

Chapelle, D., & Bathe, K. J. (1993). The inf-sup test. Computers and Structures, 47, 537–537. https://doi.org/10.1016/0045-7949(93)90340-J

Haller, H., & Krauss, S. (2002). Misinterpretations of significance: A problem students share with their teachers. Methods of Psychological Research, 7(1), 1–20. Retrieved from http://www.dgps.de/fachgruppen/methoden/mpr-online/issue16/art1/haller.pdf

LeVeque, R. J. (2002). Finite volume methods for hyperbolic problems. Cambridge University Press.

Meurer, A., Smith, C. P., Paprocki, M., Čertı́k, O., Kirpichev, S. B., Rocklin, M., … Scopatz, A. (2017). SymPy: Symbolic computing in Python. PeerJ Computer Science, 3, e103. https://doi.org/10.7717/peerj-cs.103

Mishra, S., & Spinolo, L. V. (2015). Accurate numerical schemes for approximating initial-boundary value problems for systems of conservation laws. Journal of Hyperbolic Differential Equations, 12(01), 61–86. https://doi.org/10.1142/S0219891615500034

Raymond, E. S. (1996). The new hacker’s dictionary. MIT Press.

Roache, P. J. (2004). Building PDE codes to be verifiable and validatable. Computing in Science & Engineering, 6(5), 30–38. https://doi.org/10.1109/MCSE.2004.33

Trefethen, L. N., & Bau, D. (1997). Numerical linear algebra. Society for Industrial Mathematics.